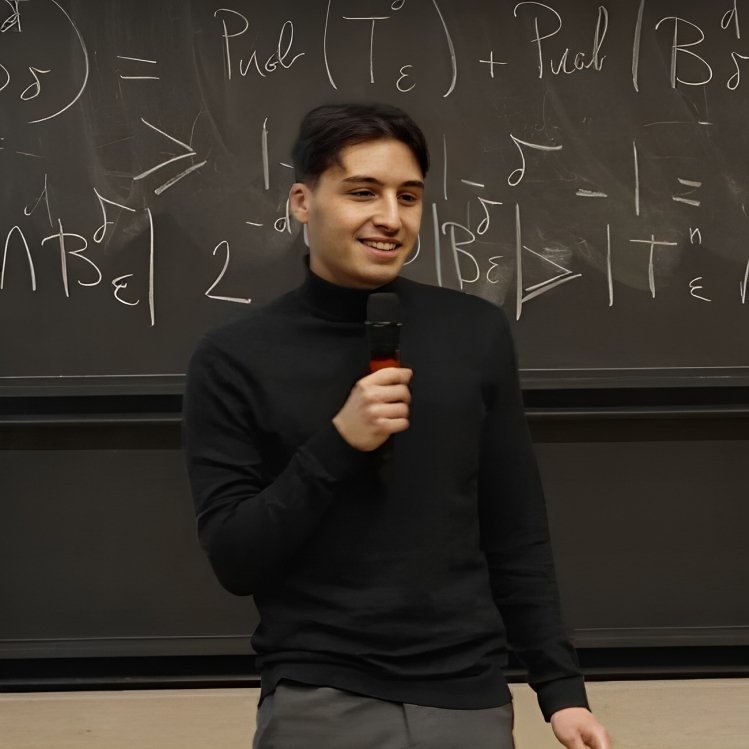Research
I am actively involved in several open-source research projects on the applications of AI for both informal and formal mathematics. My most recent completed projects are:
- Llemma: An open language model for mathematics,
- OpenWebMath: An open dataset of high-quality mathematical web text,
which both led to publications at ICLR 2024 and the MATH-AI Workshop at NeurIPS 2023 (see Publications for more details).
Below is a summary of my current and previous research projects:

 Theorem proving with tree search algorithms (since 2023)
Theorem proving with tree search algorithms (since 2023)
During my internship at the University of Cambridge under the supervision of Wenda Li, I implemented the Monte Carlo tree search algorithm for automated theorem proving with the Isabelle proof assistant, taking inspiration from Meta AI’s work. I’m now collaborating with several researchers from EleutherAI to extend this project by exploring additional tree search algorithms and integrating them with large language models trained with synthetic data.
My contributions: I re-implemented the Monte Carlo tree search algorithm to apply it to prove theorems with Isabelle.
 Human-oriented automatic theorem proving (since 2023)
Human-oriented automatic theorem proving (since 2023)
I recently joined the Human-oriented automatic theorem proving group led by Sir Timothy Gowers at the University of Cambridge. This group focuses on automatic theorem proving on the Lean proof assistant using good old fashioned AI techniques (GOFAI) rather than machine learning. This direction is motivated by the desire to improve our theoretical understanding of how mathematicians find proofs, especially since current deep learning tools often operate as “black boxes”, which makes explaining their processes challenging. This is a totally different approach to my other projects, which is what makes it interesting!
My contributions: I am currently working on tree search with GOFAI. My goal is to write GOFAI heuristics and policy functions that can be used with tree search algorithms for human-oriented ATP.
 Open-source replication of Minerva (2023)
Open-source replication of Minerva (2023)
One year ago, Google published Minerva, a powerful LLM capable of impressive mathematical reasoning. Minerva is not publicly accessible, preventing research from building on these advances. One of the key ingredients in Minerva is a closed dataset of every math document on the web, something that isn’t available to the academic community.
I recently contributed to OpenWebMath, an open-source replication of the Minerva web dataset, and Llemma, a family of open-source language models for mathematics trained on OpenWebMath, arXiv and code. Llemma exceeds Minerva’s problem solving performance on an equi-parameter basis, while covering a wider distribution of tasks, including tool use and formal mathematics.
My contributions to OpenWebMath: My work covered different parts of the project, including DOM processing, text extraction, line processing, language identification, deduplication and manual inspection.
My contributions to Llemma: I was involved in the data collection process, collecting informal mathematical data with OpenWebMath and formal mathematical data with Isabelle proofs.
 Theorem proving with GPT-3.5 (2022)
Theorem proving with GPT-3.5 (2022)
During my 2022 internship with Stanislas Polu at OpenAI, we explored the applications of GPT-3.5 for solving, generating, and auto-formalising mathematical problems using the Lean proof assistant.
Our primary aim was to compare the performance of GPT-3.5 on problems from the MATH dataset in both formal (using the Lean proof assistant) and informal settings. Building on previous work from the OpenAI team, we trained GPT-3.5 with expert iteration to tackle increasingly complex problems.
My contributions: My primary responsibilities involved dataset creation, formalising over 200 theorems in Lean to facilitate the training and testing of GPT-3.5. I also took care of the verification of the formal statements generated by GPT-3.5 for expert iteration.